Vida com o coronavírus da covid-19 – Dia 6
Pedro Pita Barros

---

Pedro Pita Barros, economista e autor Almedina, está a acompanhar diariamente a evolução do Coronavírus na economia e sociedade portuguesa, um conjunto de artigos que iremos partilhar nesta rúbrica a que o autor chamou Vida com o Coronavírus da Covid-19

A última semana foi feita às curvas e contracurvas, com diversas medidas destinadas a conter a difusão da Covid-19 a serem tomadas, culminando com a declaração do estado de emergência

No meio desta turbulência, uma discussão que normalmente seria obscura e apenas para alguns com uma costela mais nerd acabou por despertar forte atenção pública (e até paixões e ódios): saber se o crescimento da epidemia pode ser previsto com a denominada curva exponencial. Jorge Buescu, num conjunto de artigos no Observador (aqui e aqui) e num grupo de discussão no facebook, teve o mérito de lançar a discussão e chamar a atenção com as previsões de doentes que a aplicação dessa metodologia gerou (análise de regressão com utilização de curva exponencial).

Porque há formas diferentes de obter previsões e porque é conhecido que se numa fase inicial de uma epidemia esta se comporta com um padrão de crescimento exponencial, é igualmente sabido que em algum momento esse crescimento exponencial dará lugar a uma inversão, com abrandamento do crescimento (o chamado ponto de inflexão, em que a taxa de crescimento  de novos doentes passa a ser menor do que no dia anterior).

Daqui resulta que se a intenção for prever o número de doentes com covid-19 identificados pelo sistema de saúde num futuro próximo (medido em poucos dias) numa fase inicial do processo (como aquele em que nos encontramos), então a curva exponencial é uma forma simples e relativamente expedita de fazer essa previsão. E muitos têm sido os que a utilizam (aliás, se me pedirem a melhor previsão para amanhã, com base nos dados mais recentes, então essa também será a minha melhor previsão). A este respeito, deixo também aqui a ligação para o site da Associação Nacional de Médicos de Saúde Pública (ANMSP), que estabeleceu um acompanhamento da situação, com uma previsão, com a disponibilização da descrição da metodologia usada (tab “métodos” na página da ANMSP).

Diferente é se quiser prever para daqui a uma semana ou daqui a 15 dias, por exemplo. Para um horizonte mais longo, é inevitável que o processo de crescimento deixe de ser exponencial (basta pensar que no prazo de um mês não é possível ter 12 milhões de doentes de covid-19 num país com pouco mais de 10 milhões de habitantes). Este elemento é conhecido dos que estão a estimar modelos de curva exponencial para esta fase (mas com base em comentários de outras pessoas, há ainda alguma confusão sobre esse aspecto).

Daí que a previsão além dos próximos dias exija outras abordagens e esteja sujeita a mais incerteza. A utilização da curva logística como instrumento permite acomodar a redução da taxa de crescimento ao fim de algum tempo que irá necessariamente ocorrer.   A questão que se coloca em termos técnicos é qual a melhor forma de estabelecer essa curva logística – o que iremos observar será influenciado pela dinâmica natural do processo de contágio da doença e pelas políticas adoptadas com a intenção de o influenciar. A este respeito, deixo esta ilustração muito bem conseguida no Washington Post.

Claro que há alternativas à utilização da curva logística, construindo modelos mais detalhados, em que a dinâmica de contágio de pessoas saudáveis depende explicitamente de quantos indivíduos infectados circulam na população e quantos contactos realizam antes de deixar essa situação. Estas dinâmicas complicam-se quando são influenciadas por medidas adoptadas (se ainda não viu a ilustração do Washington Post, vá ao link no final do parágrafo acima). A complexidade é maior se se vier a dar o caso de que ter a covid-19 não gera imunidade futura, podendo voltar a ser contraída. A construção desse tipo de modelos demora mais tempo e exige mais informação, bem como o conhecimento técnico adequado.

A curva logística surge aqui como uma forma resumida de apanhar esses vários efeitos, e sendo a mais rápida construção uma vantagem, perde na capacidade de avaliar explicitamente efeitos das medidas distanciamento social e de contenção. Permite porém de uma forma mais rápida ter uma ideia do impacto global da infecção, em número de pessoas que previsivelmente terão covid-19.

No atual momento, dois aspectos são claros nas tentativas de construir uma curva logística: a) a sua parte inicial, tendo também um comportamento perto da curva exponencial, permite igualmente uma boa previsão a curto prazo; b) dependendo de parâmetros de caracterização, a forma de cálculo destes influencia o resultado final, podemos assim obter resultados diversos para a estimativa final do número de pessoas que contrairá a covid-19.

O meu post anterior ilustrou o primeiro ponto acima, em que para uma descrição quase idêntica da evolução inicial, a curva logística vai apresentar valores a médio prazo muito mais baixos que a curva exponencial, pela natureza explosiva desta última.

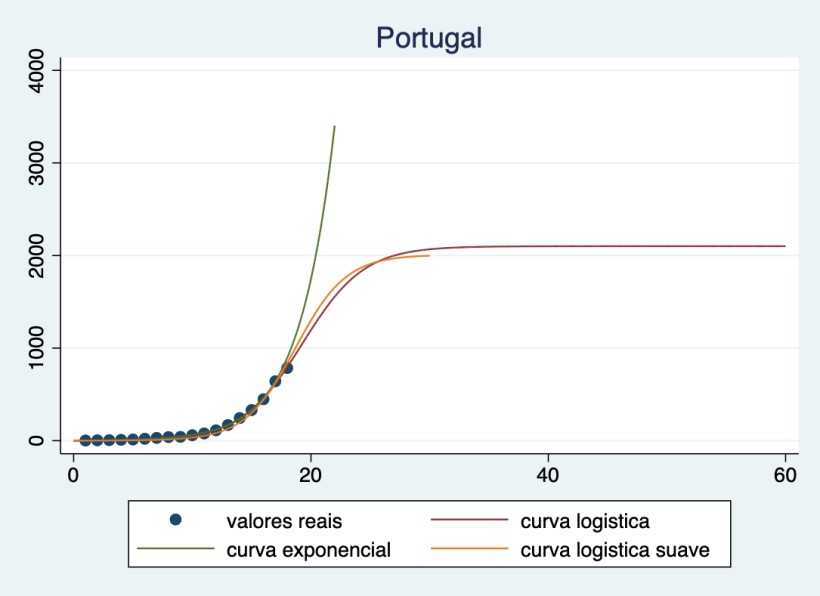
As figuras seguintes ilustram o segundo ponto: com formas diferentes de dar valores à curva logística chegamos a estimativas de pessoas com covid-19 diferentes – a figura abaixo apresenta duas dessas possibilidades (“curva logística” e “curva logística suave”, na Figura 1). Claro que conforme formos avançando no processo, a informação do que for sucedendo irá levar a uma revisão das estimativas e a uma convergência de valores. Mas esse efeito é de pouca utilidade quando se quer ter hoje uma ideia de quantas pessoas terão a covid-19, para ajudar na definição dos recursos necessários.

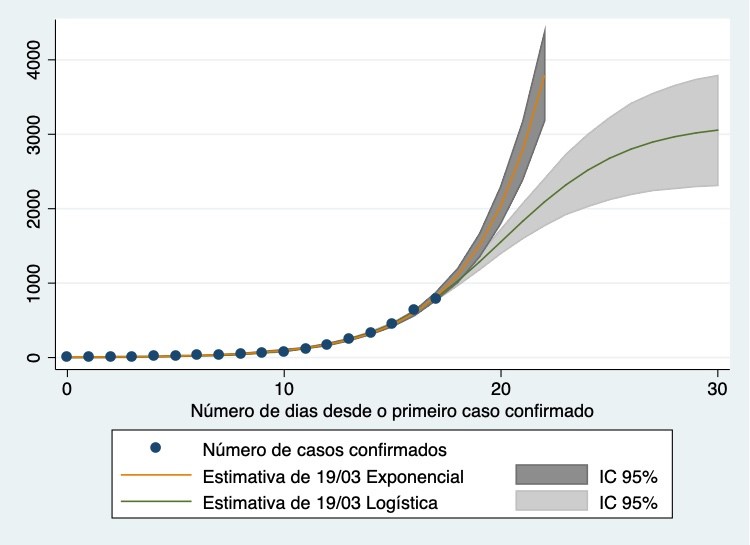
Luis Sá (Univ Minho) fez contas similares, e com uma parametrização ligeiramente diferente obteve resultados diferentes, que mudaram muito de ontem para hoje, dado o valor favorável publicado hoje (19 de março de 2020, referente a 18 de março de 2020), mostrando a sensibilidade da estimação a médio e longo prazo à informação disponível.

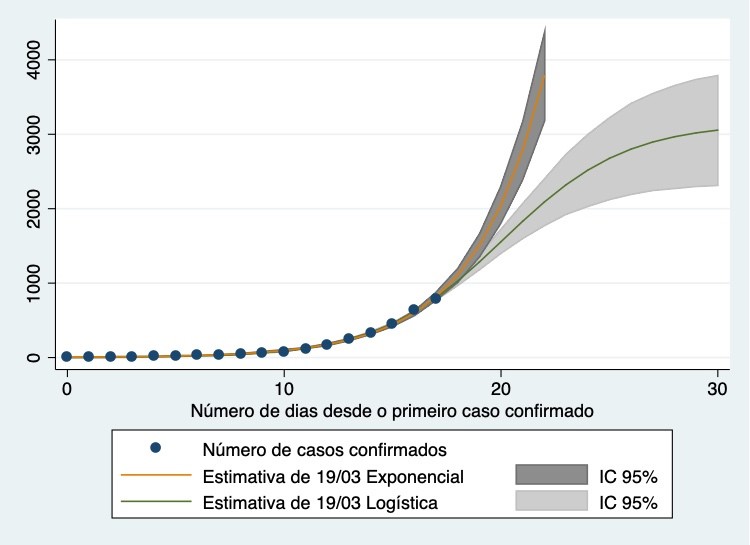
Para Itália, Gonçalo Correia Lopes (U Aveiro) tem uma comparação similar entre as duas curvas, exponencial e logística.

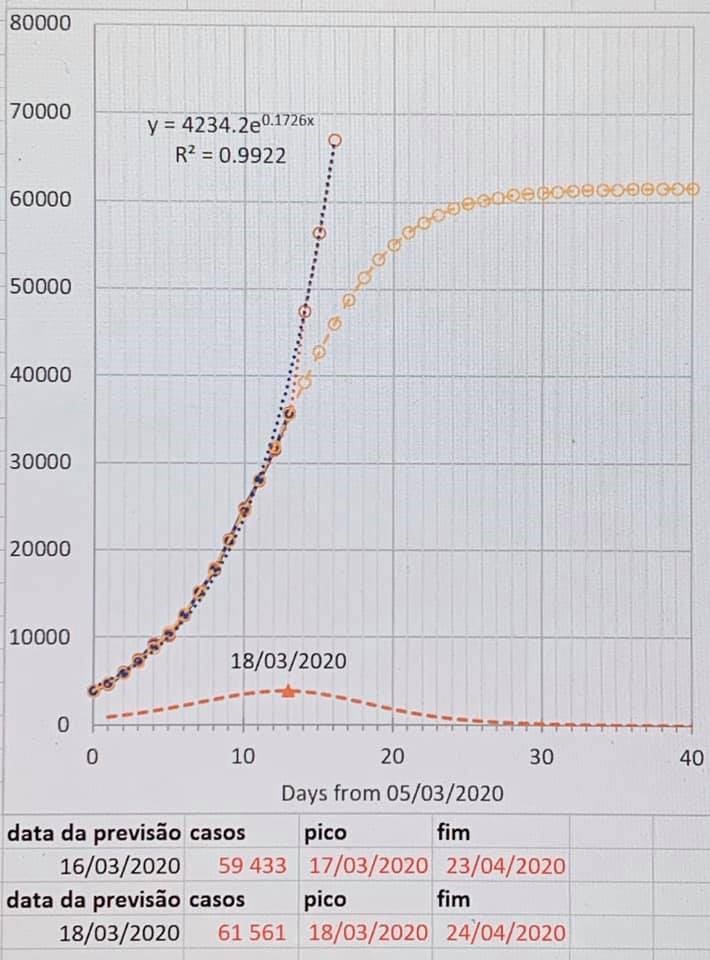
O debate que tem havido, por vezes com posições desnecessariamente extremadas, acaba por ser útil por trazer ideias, explicações, informação que é importante para estabelecer a melhor forma de prever as situações futuras. A este respeito, deixo como sugestão de leitura o texto de Alexandre Abreu no Expresso. Por exemplo, ao se elaborar um modelo matemático para descrição dos dados que é muito elegante mas impossível nos mecanismos biológicos da doença, ter um biólogo a apontar esse aspecto é relevante para rever o modelo de previsão.

Por isso, manter uma abertura intelectual e uma capacidade de escuta das visões dos outros, com sentido crítico mútuo, sem ser adversarial, ter disponibilidade de dados e fazer uma sua utilização adequada, será a  melhor forma de avançar no objectivo de uma boa previsão.

As consequências de cada um se isolar no seu mundo são ilustradas por um dos melhores gráficos que surgiu nos últimos dias, disponibilizado por Pedro Magalhães no facebook, que trazendo algum humor nos questiona sobre as oportunidades que devemos não perder para fazermos melhor estas previsões. Para que possam ser úteis a quem as quiser usar.

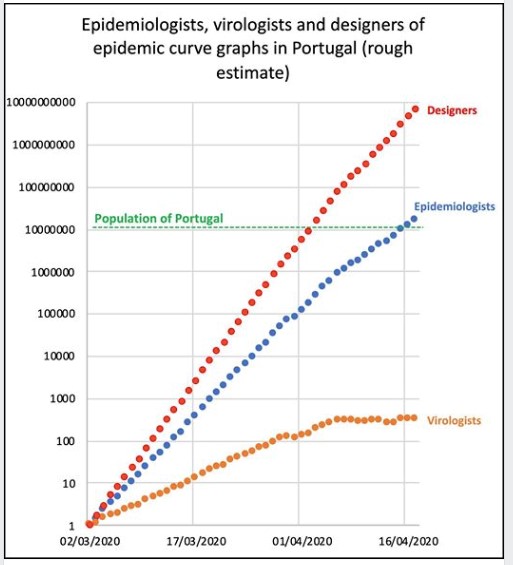
(nota: a escala dos casos é logaritmica)

A propósito desta discussão recebi muitos comentários que me fizeram pensar em argumentos e ângulos novos, e perceber limitações e possíveis extensões deste tipo de análises, bem como sugestões de leituras / videos. Deixo aqui alguns, por mero gosto pessoal (são anónimos porque me foram enviados privadamente, e pedi autorização aos autores para os divulgar, editados por mim), e sem qualquer ordem especial:

a) Creio que a tua explicação só peca por mecânica: teria sido interessante explicar porque é logística a curva. (…)
A curva começa a crescer menos e a estacionar na parte superior devido à tal “herd immunity”, ou imunidade de grupo ou de “horda”. Tal acontece quando vai diminuindo o número dos “suscetíveis”, por dentro do grupo estarem a ser muitos mais os infetados, com ou sem sintomas clínicos. É por isso que é tão importante o confinamento dos grupos, para que não haja contactos, muito menos esporádicos, de uns com os outros. A decisão do encerramento foi desastrosa em Itália por ter levado os estudantes para as residências secundárias de pais e avós, situadas a centro e sul do foco inicial. A nossa decisão, embora para mim devesse ter esperado cinco dias, foi tomada por óbvia pressão social e [levou a] encerramentos não supervisionados. estes só não foram desastrosos como em Itália por o Governo ter ordenado o confinamento quase imediato. E mesmo assim ainda iremos amargar as 36 horas entre a aplicação prática de ambas as decisões.
Informação sobre a Herd immunity pode ser obtida em Lilianfeld, Abraham, Principles of Epidemiology (…);

b) Tudo se torna mais difícil de calcular quando aquilo que se conhece são só os casos graves, havendo, pelo que se conhece da informação transmitida, muitos casos ligeiros não diagnosticados. Por cá ainda só existe indicação para testar os casos de doença respiratória grave. Países como a Alemanha e Coreia que foram mais além no testar têm uma taxa de mortalidade mais baixa.
A Itália terá uma taxa mais alta de mortalidade porque, tal a como na China, quando deu por isso já a doença estava disseminada na comunidade, havendo muito subdiagnóstico. Aliás só assim se explica como tantos estrangeiros se “infectaram” em Itália e “exportaram” a doença para os seus países, quando ainda havia relativamente poucos casos conhecidos.
Não sei se a curva de “doentes” será a mesma da dos “infectados” (formas minor+formas graves).

c) plano das autoridades italianas, aqui, com a descrição das medidas adoptadas e do seu timing.

d) Ted Talk de Bill Gates, 2015, The next outbreak? we’ re not ready – nem naquela altura, bem agora.

e) o texto de André Peralta-Santos no Público, Pandemias, instituições e open source.

f)  Sobre o meu artigo no observador (resultante do meu post anterior):  “(…) não se trata de uma questão de crença. É antes uma questão do domínio da biologia em conjunto com a matemática. Na verdade, este tipo de discussões demostra a importância de abordagens multidisciplinares. Enquanto biólogo, penso que a questão passa por analisar taxas de crescimento e ter a noção de que são os recursos do sistema que limitam o crescimento. Neste caso específico, é a “disponibilidade de humanos” que faz o factor exponencial ser maior ou menor. Assim, os modelos têm de ser ajustados no dia a dia e para isso é importante ter bons números, para ajustar as previsões e poder ter dados mais fiáveis. Certo que os modelos são dependentes da quantidade dos dados existentes, por isso a importância de integrar conhecimento de diferentes disciplinas à priori, para evitar más previsões a longo prazo.”

g) duas sugestões de leitura no facebook: Luis Vicente (aqui) e Filipa Vala (via Guadalupe Simões) (aqui), além do grupo criado pelo Jorge Buescu (aqui) (acesso por autorização), onde se encontram muitos comentários interessantes.

Em resumo, a) muitas das diferenças que surgem na discussão resultam de perspectivas distintas- prever os próximos dois ou três dias, versus perceber o que será a dimensão total; b) a incerteza a prever a mais de dois ou três dias é ainda bastante grande; c) a discussão tem tido uma considerável participação cívica.

Para os próximos dias, parece-me importante continuar o caminho de redução iniciado de contenção e evitar a ansiedade criada por estar sempre a vigiar a revelação de novos números (uma vez que uns dias serão mais positivos e outros mais negativos).

---

Anexo Técnico:

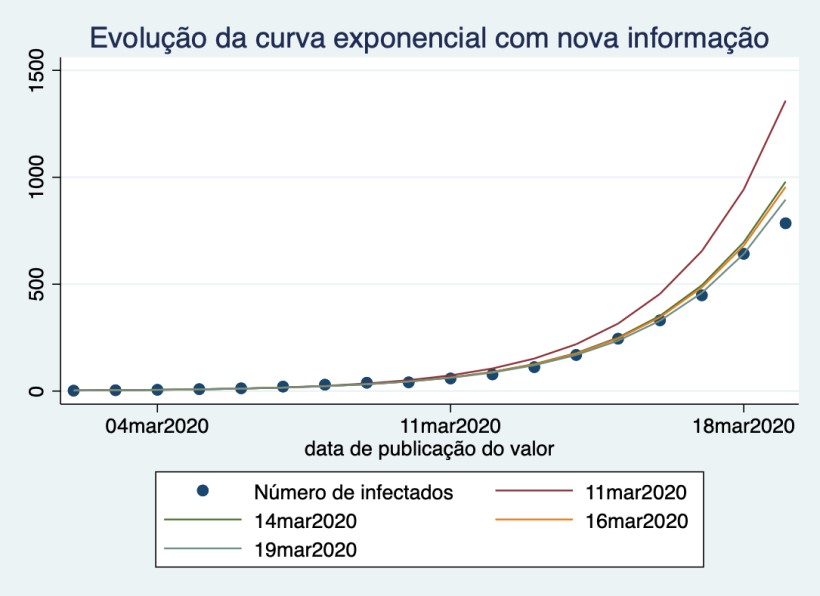
A evolução da curva exponencial: tem-se falado da curva exponencial como sendo uma única curva. Na verdade, cada vez que sai um novo valor, cada dia, para o número de doentes em Portugal, é, ou deve ser, atualizada a curva. Curiosamente, tem havido uma evolução sucessiva da curva exponencial, tornando-se menos exponencial ao longo dos dias. Significa que há uma semana atrás a previsão do valor de doentes para o dia de hoje é muito maior do que o valor realmente observado, e maior do que o valor previsto com base em toda a informação até ontem. Este sucessivo abaixamento da curva exponencial é ele próprio um sinal favorável, ainda que bastante ténue ainda.

A figura seguinte ilustra essa evolução, enquanto o quadro apresenta a diferença crescente entre a projecção da curva exponencial que era possível estimar há uma semana, e o que é a realidade de hoje.

		Previsão segundo a curva exponencial na data :
	Casos Reais	10 Março 2020	13 Março 2020	16 Março 2020	18 Março 2020
11/03/2020	59	73
12/03/2020	78	106
13/03/2020	112	152	126
14/03/2020	169	219	178
15/03/2020	245	316	250
16/03/2020	331	455	352
17/03/2020	448	655	495	476
18/03/2020	642	943	696	667
19/03/2020	785	1358	979	935	896

É interessante ver qual o erro de previsão para os dois últimos dias conhecidos (18 e 19 de Março 2020), em que o erro de previsão aumenta consideravelmente quando se usa estimativas da curva exponencial da semana passada – utilizando a informação até 11 de março de 2020 para estimar uma curva exponencial, e prevendo para uma semana depois, o valor estimado de casos é de 1358, o valor real foi 785, que é cerca de 58% do valor previsto. Há por isso um desvio importante na previsão.

19/03/2020	10 Março 2020	13 Março 2020	16 Março 2020	18 Março 2020
erro de previsão	573	194	150	111
erro (%)	57,79%	80,15%	83,97%	87,66%
18/03/2020	10 Março 2020	13 Março 2020	16 Março 2020
erro de previsão	301	54	25
erro (%)	68,07%	92,20%	96,24%

Métodos: curva logistica

A equação estimada da curva logística tem a seguinte forma y = b1 * (1+exp(-b2*(x – b3))^(-1).

Foram usados dois métodos de estimação, que produzem resultados não muito diferentes. O primeiro envolveu optimização não-linear para obter os melhores valores possíveis dos parâmetros da curva, de forma a reproduzir as observações que já existem. O segundo método consistiu em primeiro estimar dois parâmetros (b2 e b3) de forma a reproduzirem da melhor forma possível a taxa de crescimento observada em Portugal. Tendo estas estimativas, recuperou-se, utilizando o valor absoluto de doentes em Portugal por dia, o parâmetro de escala final, que é essencialmente similar. A tabela seguinte reproduz os valores obtidos para a estimativa pontual.

	Versão 1	Versão 2
b1	2100	2008
b2	0,385	0,469
b3	19,283	18,708

Artigo originalmente publicado a 19 de março de 2020, em https://momentoseconomicos.com/2020/03/19/curvas-e-contracurvas-vida-com-o-coronavirus-6/